Lors du second quadrimestre, on nous a demandé de modéliser un circuit électronique, le Joule Thief pour les connaisseurs. Le modèle devait être capable de prédire la fréquence, les tensions à certains endroits du circuit et le rendement. Nous avons fait tout ça sur MatLab, le fameux logiciel de l’ingénieur. Après quelques mois de prise en main et une bonne dizaine de scripts en place, j’écris ce petit billet de trucs et astuces très (très) simples.
Vecteurs et variables
MatLab est habitué à travailler avec des vecteurs et des matrices, il est très rapide pour les manipuler. On essaiera toujours de les utiliser au maximum.
a = 4
On peut simplement attribuer la valeur 4 à la variable a.
X = [1 4 5 6]
On crée un vecteur ligne X dont les entrées sont 1, 4, 5 et 6.
U = X'
Le nouveau vecteur U est la transposée du vecteur X. Le vecteur ligne devient un vecteur colonne.
W = X*U
Multiplication matricielle de X par U.
Z = a .* X
Multiplication de toute les entrées du vecteur X par le scalaire a.
Note : les commentaires se font en utilisant le %, et l’usage du ; est le suivant : si l’on veut afficher la ligne dans le Command Window, il ne faut pas en mettre. Mais, de manière générale, on en place à la fin de la plupart des lignes.
Les graphiques
Touchons maintenant à ce qui est beaucoup plus intéressant avec MatLab : les graphiques. MatLab regorge de fonctions différentes pour dessiner (plotting en anglais) des graphes ; je vous montre la plus simple.
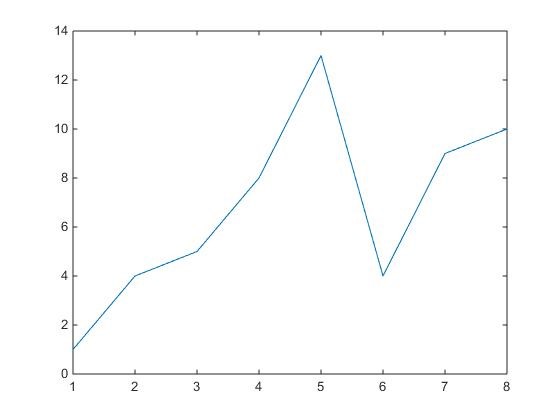
X = [1 2 3 4 5 6 7 8]
Y = [1 4 5 8 13 4 9 10]
plot(X, Y)
Le vecteur X contient les abscisses et le vecteur Yles ordonnées. Matlab reliera tous les points par des droites.
Les différents points sont : (1,1) (2, 4) (3, 5) (4, 8) (5, 13) (6, 4) (7, 9) et (8,10). Voyez-vous maintenant comment fonctionne la fonction plot?
On peut rajouter un titre et des axes.
title('Graphique inutile de démonstration');
xlabel('Masse de riz (kg)');
ylabel('Température du frigo (°C)');
On peut également changer le style de trait :
plot(X, Y, '.', 'MarkerSize', 30)
plot(X, Y, '-.')
La première ligne dessinera des gros points (taille 30), et la seconde des pointillés entre les points. Ce genre de manipulation est très utile, par exemple pour dessiner des graphiques expérimentaux.
Qu’en est-il de dessiner des fonctions ? Essayez ce bout de code :
X = linspace(0, 2*pi, 100)
Y = sin(X)
plot(X, Y)
La fonction linspace va créer un vecteur contenant 100 entrées réparties uniformément entre 0 et et 2π. Cette fonction est très rapide et très efficace en MatLab ; chaque fois qu’il est possible de l’utiliser, je vous encourage à le faire.
X = linspace(0, 2*pi, 100) %abscisses
Y = sin(X) %fonction f(x) = sin(x)
Z = X.^2 %fonction f(x) = x²
R = X.^2 + 2.*X + 4*pi %fonction f(x) = x² + 2x + 4Pi
plot(X, Y)
hold on;
plot(X, Z)
hold on;
plot(X, R)
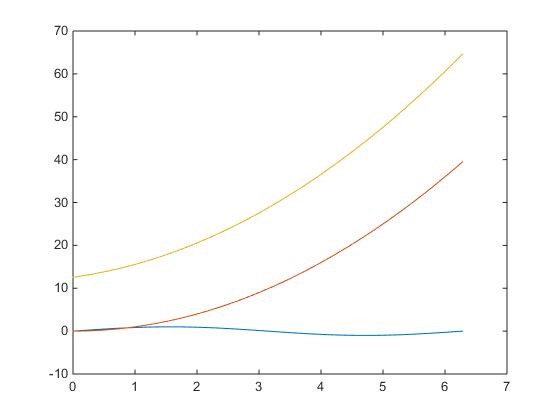
Quelques exemples de fonctions à dessiner avec cette méthode. La fonction hold on permet de dessiner sur le même graphe. Pour le faire sur un nouveau graphe, il faut utiliser figure. Pour écraser les graphiques précédents du tableau, hold off. Le rendu est sympathique !
Résolution d’équations
On continue les fonctions utiles et vraiment simples d’utilisation ! Admettons que l’on cherche les racines du polynôme x2 + 2x + 4. En quelques lignes, MatLab le fait pour nous.
syms x
eq = x^2 + 2*x - 4
solve(eq);
syms permet de déclarer que x est un symbole, une variable qui ne prendra jamais de valeur. Dans la variable eq, nous insérons notre équation avec le sous entendu = 0, et solve la résout aussitôt.
Tips du tips :
solve(eq, t)
Résout l’équation selon la variable t ; on n’a pas forcément qu’une inconnue !
answer = solve(eq);
eval(answer)
Affiche la valeur numérique de la réponse.
answer = solve(eq)
simplify(answer)
Simplifie au maximum la réponse, par exemple pour des grosses fractions.
pretty(answer)
Affiche de manière stylée la réponse à l’écran. Très pratique quand on a des fractions qui dépendent d’une dizaine de paramètres, et qu’une vingtaine de parenthèses et d’exposants interviennent.
Retour en enfance :
syms a b c x
eq = a*x^2 + b*x + c
answer = solve(eq, x)
pretty(answer(1))
pretty(answer(2))
Et le résultat sorti dans le Window Command est le suivant :
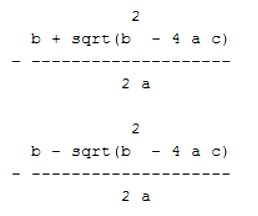
Résoudre d’abord en symbole et ensuite en numérique est vraiment très pratique dans nos études. On est souvent amené à déterminer des expressions de telle chose en fonction de tels autres paramètres, et ensuite de remplacer ces paramètres pour trouver une réponse finale. Ci-dessous un exemple adaptable à nos nombreux problèmes :
syms a b c x;
eq = a*x^2 + b*x + c;
answer = solve(eq, x);
pretty(answer(1));
pretty(answer(2));
a = 5; %On fixe tous les paramètres
b = 3;
c = -12;
eval(answer(1))
eval(answer(2))
Ressortant en une fraction de seconde ans = –1.8780 et ans = 1.2780. MatLab est vraiment illimité, et c’est un plaisir de travailler avec lui au quotidien quand on le maîtrise plutôt bien !
Dérivée analytique
On va vite parler de dérivée analytique d’une expression ; rien de plus simple pour MatLab !
syms x;
f = 2*x^2 + 4*x + 8
df = diff(f, x)
Instantanément MatLab nous envoie la dérivée du polynôme 2x2 + 4x + 8, c’est-à-dire 4x + 4. Notez que dans diff(f, x),x est bien la variable par rapport à laquelle on veut dériver. Cette fonction nous permet donc de faire des partielles !
Pour la route, quelques codes d’exemples :
syms x;
f = 2*x^2 + 4*x + 8
f_prime = diff(f, x)
x = linspace(-10,10,1000);
y = eval(f);
y_prime = eval(f_prime);
plot(x, y); hold on;
plot(x, y_prime);
Dessiner le polynôme et sa dérivée, rendu :
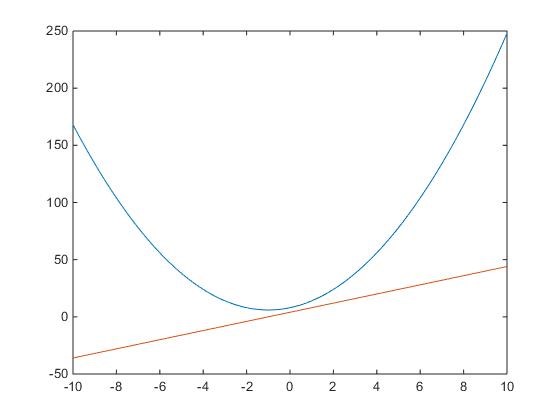
Quelques exemples
Résoudre un système du second degré :
syms x y;
eq1 = (x-6)^2+ (y-6)^2 - 16
eq2 = (x-1)^2 + (y-1)^2 - 26
[x,y] = solve([eq1, eq2], [x, y])
Chronométrer l’exécution de votre code :
tic
%
% code à exécuter
%
toc